Quiero hacerlo esta noche..... Contigo: Círculo de Mohr

sábado, 15 de noviembre de 2008

Círculo de Mohr

No os podeis imaginar el trabajo de calculo que ahorra este sistema a la hora de calcular las acciones que tienen lugar sobre un solido deformable un un problema de elasticidad lineal.

Aqui os dejo su funcionamiento:

El círculo de Mohr es una técnica usada en ingeniería para representar gráficamente un tensor simétrico (de 2x2 o de 3x3) y calcular con ella momentos de inercia, deformaciones y tensiones, adaptando los mismos a las características de un círculo (radio, centro, etc). También es posible el cálculo del esfuerzo cortante máximo absoluto y la deformación máxima absoluta.

Este método fue desarrollado hacia 1882 por el ingeniero civil alemán Christian Otto Mohr (1835-1918).

Círculo de Mohr para esfuerzos

Caso bidimensional

Círculo de Mohr para esfuerzos.

En dos dimensiones el círculo de Mohr permite determinar la tensión máxima y mínima, a partir de dos mediciones de la tensión normal y tangencial sobre dos ángulos que forman 90º:

$\begin{cases} \mbox{medida 1} & (\sigma_x, \tau) \\ \mbox{medida 2} & (\sigma_y, -\tau) \end{cases}$

NOTA: El eje vertical se encuentra invertido, por lo que esfuerzos positivos van hacia abajo y esfuerzos negativos se ubican en la parte superior.

Usando ejes rectangulares, donde el eje horizontal representa la tensión normal $\left( \sigma \right)$ y el eje vertical representa la tensión cortante o tangencial $\left( \tau \right)$ para cada uno de los planos anteriores. Los valores del círculo quedan representados de la siguiente manera:

Centro del círculo de Mohr:

$C:= (\sigma\ _\mbox{med},0) = \left(\frac {\sigma\ _x + \sigma\ _y} {2}, 0\right)$

Radio del círculo de Moh r:

$r:= \sqrt{ \left ( \frac { \sigma\ _x - \sigma\ _y } { 2 } \right ) ^2 + \tau\ ^2_{xy} }$

Las tensiones máxima y mínima vienen dados en términos de esas magnitudes simplemente por:

$\sigma_\mbox{max} = \sigma_\mbox{med} + r \qquad \sigma_\mbox{min} = \sigma_\mbox{med} - r$

Estos valores se pueden obtener también calculando los valores propios del tensor tensión que en este caso viene dado por:

$\mathbf{T}\vert_{x,y} = \begin{bmatrix} \sigma_x & \tau \\ \tau & \sigma_y \end{bmatrix}$

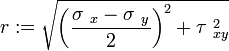
2 comentarios:

Sevilla en Salsa dijo...: Uffff... que nivel.

Parece copiado de algun sitio... voy a leerlo de nuevo a ver si me entero de que va... ya que soy físico; 22 de junio de 2009, 8:18
Alex | Fontaneros Rivas dijo...: pero mis respeto para el señor; 30 de noviembre de 2012, 8:49

Publicar un comentario

sábado, 15 de noviembre de 2008

Círculo de Mohr

Círculo de Mohr para esfuerzos

Caso bidimensional

2 comentarios:

Votame !!